Cette version du forum n'est désormais accessible que pour lire les passionants échanges et partage de techniques qui ont déjà été rédigées ici.
Pour participer aux échanges interscouts, merci d'utiliser
| Aller à Page Précédente 1|2|3|4|5|6|7 Page suivante |
| Auteur | lois mathématiques !!!!! (Murphy et autres génies) |
| Rantanplan canidé
Nous a rejoints le : 19 Fév 2004 Messages : 4 261 Réside à : France-désert |
 94      |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
95 |
| Orignal E Élan
Nous a rejoints le : 11 Janv 2006 Messages : 1 895 Réside à : le ventre de maman |
96 |
| fennec78 Joyeux membre
Nous a rejoints le : 26 Juil 2005 Messages : 329 |
97 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
98 |
| Rantanplan canidé
Nous a rejoints le : 19 Fév 2004 Messages : 4 261 Réside à : France-désert |
99 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
100 |
| Fab Membre familier
Nous a rejoints le : 11 Mai 2005 Messages : 493 Réside à : Rosny-sous-bois (Est parisien) |
101 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
102 |
| Orignal E Élan
Nous a rejoints le : 11 Janv 2006 Messages : 1 895 Réside à : le ventre de maman |
103 |
| Rantanplan canidé
Nous a rejoints le : 19 Fév 2004 Messages : 4 261 Réside à : France-désert |
104 |
| Rantanplan canidé
Nous a rejoints le : 19 Fév 2004 Messages : 4 261 Réside à : France-désert |
 105 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Citation: Prouve moi qu'on obtient bien quelque chose de non nul ! Citation: Viens me parler de rigueur après ça ! Rigoureusement parlant, on n'a pas le droit d'écrire 10^-inf. A l'extrême limite on pourrait poser 10^-inf=lim(x->inf)10^-x. Tu as raison on ne devrait pas, si on fait une approximation, utiliser le signe =. On devrait écrire 1-0,9999999999...=10^-inf. Donc par définition 1-0,9999999999...=lim(x->inf)10^-x. D'où 1-0,9999999999...=0 CQFD 106  |
| Jack Membre confirmé
Nous a rejoints le : 19 Juin 2005 Messages : 1 520 Réside à : Whitechapel, London |
Citation: *et * semblent pas trop mal... On la donne ou la réponse alors ?? 107 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
Citation: tu lui envoie par MP. Aller un grand classique et envoyer moi la réponse par MP: faites un 4 triangles équilatéraux avec 6 allumettes.  108 |
| Orignal E Élan
Nous a rejoints le : 11 Janv 2006 Messages : 1 895 Réside à : le ventre de maman |
Citation:Erreur, c'est à toi (ou à un autre, d'ailleurs) de prouver que c'est nul, pas le contraire. Et tu ne le fais pas, puisque tu pars d'une approximation. 109 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Erreur. Je n'ai rien affirmé concernant ce dont parle Elecscout. S'il affirme que ce n'est pas nul c'est qu'il doit pouvoir le démontrer. Parce que j'aimerai bien savoir ce qu'il intègre.
D'ailleurs, je reformule ma question Citation: On obtient combien ? Quant à dire que je n'ai rien démontré, je reprend ma démonstration 1-0.9999...=10^-inf or par définition, 10^-inf= lim(x->inf)10^x et lim(x->inf)10^x=0 donc 1-0.9999...=0 rigoureusement ! 110 |
| sarigue Didelphidé
Nous a rejoints le : 04 Janv 2004 Messages : 5 895 Réside à : Vie à Rueil-Malmaison, Scout ailleurs |
NON.
10^-inf = 0,000000...0001 (avec une infinité de 0 entre la virgule et le 1) Tandis que 0 = 0,000000... (avec une infinité de 0 derrière la virgule) Tu vois bien que c'est différent!! On intégrant les petites fraction, on obtient quoi? Ca dépend de combien à combien tu intègres (l'intégration est bornée)!! De manière générale: INTEGRALE[a,b](f(x)dx) = F(b) - F(a), où F(x) est la fonction primitive de la fonction f(x). Exemple: INTEGRALE[0,3](dx) = 3 (car dx = 1.dx et la primitive de la fonction f(x)=1 est F(x)=x. Donc, l'intégrale est F(3) - F(0) = 3 - 0 = 3. Et on a bien 3 > 0) Rappel: Integrer les dx, c'est en fait sommer ces dx sur l'intervalle définie. Graphiquement, cela correspond à la surface limitée par l'axe des abscisse, la courbe représentative de la fonction (ici, la fonction f(x)), la droite perpendiculaire aux abscisses en a (ici, la droite x=a) et la droite perpendiculaire aux abscisse en b (ici, la droite x=b) C'est donc aussi sommer une infinité de rectangles de largeur dx et de hauteur f(x). 111 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Citation: NON 10^-inf=lim(x->inf)10^-x Ceci étant dit, c'est en réalité un problème de convention. La convention habituelle veut qu'on n'écrive pas lim(x->inf)SOMME(n=1 à x) (9*10^-x)=0.99999... Comme je le disais, c'est un problème de notation (sur la signification des ...) Pour plus de détails 112 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
Cette phrases est indémontrable.
^ | allez y pour le faire. 113 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Dans le même genre :
Cette phrase est un mensonge. 114 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
Citation: tiens si tu aimes réfléchir... pour ta phrase je m'en occupe: Faux!!! c'est un mensonge!! 
115 |
| Orignal E Élan
Nous a rejoints le : 11 Janv 2006 Messages : 1 895 Réside à : le ventre de maman |
Citation: Citation: Y a pas un problème, SER? Parce que on ne pas écrire un truc, mais tu en donne la définition toi même! J'ai du mal à comprendre! 116 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Orignal, les notations en mathématiques sont des conventions. Par convention on n'utilise l'infini que dans l'expression des limites. Mais une convention ça peut se changer à condition de bien définir les notations que tu utilises. En particulier la seule chose que peut signifier 10^-inf c'est lim(x->inf)10^-x. 117 |
| Jack Membre confirmé
Nous a rejoints le : 19 Juin 2005 Messages : 1 520 Réside à : Whitechapel, London |
Vincent, quand tu dis que
1=0,99999999... et que tes sources disent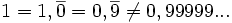 
C'est contradictoire non ? De plus, que fais du fait que la fonction 10^x soit strictement positive pour x appartenant à R ? Quand elecscout (et moi) écrit 0,0000....0001 c'est qu'il s'agit un nombre fini. C'est la méthode qu'a utilisé mon prof pour faire sentir comment marche une limite. De plus, généralement, tu tends vers l'infini, mais tu ne l'attends pas, par définition de l'infini. Vu qu'il y a des non matheux, c'est une manière de faire comprendre quelque chose et ainsi juger si 1=0,9999999... ou pas. (tout dépend de comment on se représente l'infini) Il n'y a d'ailleurs aucun interet à se visualiser l'infini.(enfin, si, il y en a, mais bon, on va faire comme si) Pour les applications, l'infini est toujours défini par une valeur. Sinon, je dis 4 et 3 ! 118 |
| Dr. Cerf Vincent Cervidé
Nous a rejoints le : 25 Oct 2001 Messages : 5 338 Réside à : Paris |
Citation: Non, c'est un simple problème de notation. Ce que j'ai essayé de faire comprendre depuis le début c'est que ce que je note 0,999999... c'est ce qui est noté dans l'article 0,9_ (je ne sais pas mettre la barre au dessus du 9 en html). Je ne connaissais d'ailleurs pas cette notation sinon je l'aurais utilisée. Citation: Ben justement, je passe à la limite. 119 |
| Gage Membre actif
Nous a rejoints le : 23 Janv 2007 Messages : 98 Réside à : Sèvres |
J'avais pensé à 4 et 3, mais un raisonnement poussé montre que ce n'est pas 4 et 3. Pour le moment, mon hypothèse la plus sérieuse est 9 et 2. Je n'en suis ps certain à 100%, c'est juste que c'est le seul couple dont je n'ai pas encore démontré l'impossibilité.
On appelle méta-jeux cette catégorie -passionnante- de jeux dans lesquels on s'intéresse au moins autant aux participants qu'aux données du jeu. Il est intéressant de noter que balancer une réponse comme ça n'apporte pas grand-chose, ce qui compte c'est le raisonnement derrière  .
Pour ce qui est de 0,9999... = 1, plusieurs arguments permettent d'affirmer (et de démontrer) qu'effectivement, 0,9999... = 1 et que ce n'est pas qu'une vue de l'esprit. - La technique du 10X = X+9 est une technique fréquemment utilisée, à la main, pour identifier une fraction à partir de son seul développement décimal (on appelle développement décimal la répétition infinie d'une séquence de longueur finie de chiffres obtenue en effectuant la division). Par exemple, on peut identifier par cette technique la fraction correspondant à 0,1428571428571428571... - C'est l'existence du développement décimal de 1 qui permet de le ranger dans la catégorie des nombres rationnels : les nombres comportant, après un certain chiffre, la répétition infinie d'une séquence de chiffres de longueur finie. Ce chiffre se situe parfois loin après la virgule. Enfin, j'ai moi-même une énigme à proposer : Vous êtes étudiant en maths. Comme chaque année, un de vos profs décerne une récompense, purement honorifique, à son meilleur étudiant. Problème : cette année, vous êtes parmi les 3 ex-aequo ! Il a donc imaginé l'épreuve suivante pour vous départager : il vous fait tous les 3 asseoir sur une chaise et vous met un chapeau sur la tête, de façon que chacun ne peut voir que les chapeaux des 2 autres étudiants. Ils sont tous les deux rouges (les chapeaux, pas les étudiants ). Il vous demande alors "Vous devez lever la main si vous voyez au moins un chapeau rouge. Le premier qui trouvera la couleur de son chapeau aura gagné".
Les 3 étudiants lèvent la main. 20 minutes passent et personne ne trouve la couleur de son chapeau. - Quelle est la couleur de votre chapeau ? 120 |
| frère brun loup brun
Nous a rejoints le : 30 Mai 2004 Messages : 211 Réside à : Brest |
je fais comment pour te répondre je crois que j'ai trouver. 121 |
| Gage Membre actif
Nous a rejoints le : 23 Janv 2007 Messages : 98 Réside à : Sèvres |
Envoie-moi un MP. Note bien que ce qui compte, c'est le raisonnement, pas la réponse ;).
Monsieur l'admin, il faudrait une balise qui permette de choisir si on veut rendre une réponse lisible ou pas. Par exemple la possibilité d'écrire en blanc (sur fond écru, on est obligé de sélectionner le texte avec la souris pour le voir), ou alors une balise [spoil] comme ça existe sur certains forums de cinéphiles pour obliger la personne qui lit à cliquer pour afficher la réponse. Comme ça tout le monde peut choisir de lire, et peut aussi choisir de ne pas lire. 122 |
| Aller à Page précédente 1|2|3|4|5|6|7 Page suivante | ||
 |
 |
 Signaler
|
   | technique |
   | bonne humeur |
Ecussons
Posté le: 18-01-2007 à 19:44
